Инвариант

ИНВАРИАНТ (от латинского invarians, родительный падеж invariantis - неизменяющийся), отображение φ совокупности объектов М, на которой задано отношение эквивалентности р, в другую совокупность N, постоянное на каждом из классов эквивалентности М по р (точнее, φ - инвариант отношения эквивалентности р на М). Если Х - объект из М, то говорят, что φ(Х) - инвариант объекта Х. Понятие инварианта является одним из важнейших в математике, поскольку оно связано с задачами классификации объектов того или иного типа. По существу, цель всякой математической классификации - построение некоторой полной системы инварианта (по возможности наиболее простой), т. е. такой системы, которая разделяет любые два неэквивалентных объекта из рассматриваемой совокупности. Термин «инвариант» ввёл Дж. Сильвестр (1851).

Простейшими примерами инварианта являются так называемый инвариант нераспадающихся кривых 2-го порядка на евклидовой плоскости. Пусть М - множество всех таких кривых, а р отношение эквивалентности на М, определённое правилом: Г є М эквивалентна Г’ є М тогда и только тогда, когда Г ‘ получается из Г движением (т.е. изометрией) плоскости. Если

- уравнение кривой Г є М в какой-либо декартовой системе координат, то числа

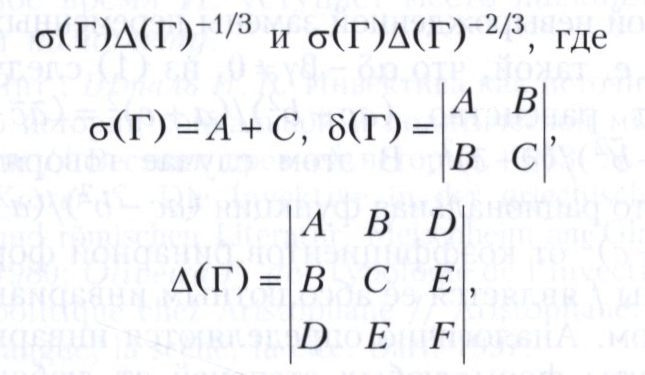
не зависят от выбора системы координат (хотя само уравнение линии Г - зависит) и кривые Г, Г’ є М эквивалентны тогда и только тогда, когда

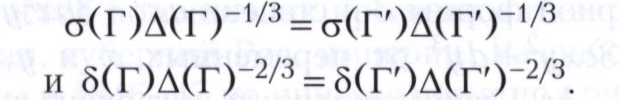
Иначе говоря, отображения σΔ^-1/3 и δΔ^-2/3 множества М в множество N всех действительных чисел являются инвариантами отношения эквивалентности р (и, более того, образуют полную систему инвариантов); эти отображения и называют инвариантами нераспадающихся плоских кривых 2-го порядка. Значения этих инвариантов на конкретной линии позволяют определить тип этой кривой (эллипс, гипербола, парабола).

Другой классический пример - двойное отношение упорядоченного набора четырёх различных точек, лежащих на одной прямой в действительном проективном пространстве. Двойное отношение не изменится, если подвергнуть эти точки проективному преобразованию всего пространства. В этом примере М - множество упорядоченных четвёрок точек проективного пространства, лежащих на одной прямой; отношение эквивалентности р на М определяется по правилу: наборы F, F’ є М эквивалентны тогда и только тогда, когда F переводится в F’ проективным преобразованием пространства. Взятие двойного отношения определяет изображение М в множество действительных чисел N. Это отображение является инвариантом отношения р (и, более того, образует полную систему инвариантов); именно в этом смысле говорят, что двойное отношение - инвариант четырёх точек (относительно проективной группы). Смотри также Инвариантов теория.

В. Л. Попов.