Интеграл

ИНТЕГРАЛ, одно из важнейших понятий математического анализа, возникшее в связи с потребностью, с одной стороны, отыскивать функцию по её производной, например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки, с другой -вычислять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п. При этом различают неопределённый и определённый интегралы (смотри Интегральное исчисление). Термин «интеграл» впервые встречается у Я. Бернулли (1690).

Для непрерывной функции f(х) и чисел а<b определённый интеграл с нижним пределом а и верхним пределом b по О. Коши (1823)

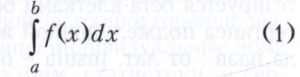
вводится следующим образом. Отрезок [а, b] произвольным образом разбивается точками х₀ , x₁, x₂, … x_n-1, х_n таки­ми, что

на частичные отрезки   [x_k-1, x_k], k = 1, 2n, и при произвольном выборе точек ζ_k на отрезках [x_k-1, x_k] составляются интегральные суммы

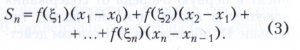
Определённым интегралом называется предел сумм S_n при стремлении к нулю наибольшей из разностей x_k - x_k-1. Для непрерывных функций этот предел существует и не зависит ни от разбиений (2), ни от выбора точек ξ_k на частичных отрезках и его можно вычислять по формуле Ньютона - Лейбница

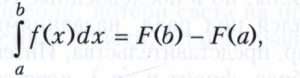
где F - любая первообразная функции f.

Интеграл Римана. О. Коши применял своё определение интеграла только к непрерывным функциям. Б. Риман предложил (1853) определять интеграл (1) как предел сумм (3) при стремлении к нулю наибольшей из разностей x_k - x_k-1 во всех случаях, когда этот предел однозначно определён, а также исследовал условия существования такого интеграла. Законченную форму этим условиям придал А. Лебег (1902), используя введённое им понятие меры множества. Оказалось, что для интегрируемости в смысле Римана функции f(x) на отрезке [а, b] необходимо и достаточно, чтобы функция f(х) была ограничена на отрезке [а, b] и чтобы множество её точек разрыва на этом отрезке имело меру Лебега, равную нулю. Для такой функции f(х) справедлива формула Ньютона – Лейбница

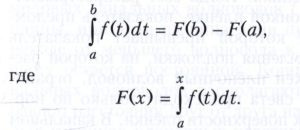
При этом в точках непрерывности функции f, т. е. всюду на отрезке [а, b], кроме, быть может, множества точек, имеющего меру Лебега, равную нулю, справедливо равенство F’(х)=f(х).

Ж. Г. Дарбу предложил (1879) вместо интегральной суммы (3) рассматривать верхнюю сумму s̅_n и нижнюю сумму S_n, определяемые равенствами

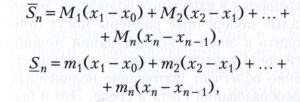
в которых М_k - точная верхняя, а m_k - точная нижняя грани значений функции f(х) на отрезке [x_k-1, x_k], k = 1, 2, ..., n. Для любой ограниченной на отрезке [а, b] функции f(х) существует точная нижняя грань по всем разбиениям (2) верхних сумм s̅_n, обозначаемая символом Ī и называемая верхним интегралом Дарбу, и точная верхняя грань по всем разбиениям (2) нижних сумм S_n, обозначаемая символом I и называемая нижним интегралом Дарбу. Необходимым и достаточным условием интегрируемости по Риману ограниченной функции f(х) является равенство Ī = I верхнего и нижнего интегралов Дарбу. При выполнении этого равенства общее значение I = I = Ī совпадает с интегралом в смысле Римана.

Интеграл Лебега. Введённое А. Лебегом понятие меры множества привело (1902) к значительному расширению понятия интеграла. Пусть функция f(х) ограничена на отрезке [а, b], то есть существуют действительные числа А и В такие, что все значения у = f(х) этой функции удовлетворяют неравенствам А≤у<В. При произвольном разбиении промежутка А≤у<В точками у₀,у₁,у₂,…y_n-1,у_n,

на частичные промежутки [у_k-1, y_k),k = 1, 2, ..., n, и при произвольном выборе значений % таких, что у_k-1 ≤ η_k < y_k составляется сумма

в которой E_k, k=1, 2, ..., n - множество тех значений х, для которых y_k-1 ≤ f(х) < y_k, а μ(E_k) - мера Лебега множества Е_к. Интегралом  (1) в смысле Лебега от ограниченной функции f(х) называется предел сумм S_n при n → ∞ при условии, что наибольшая из разностей y_k-y_k-1 стремится к нулю.

Для интегрируемости по Лебегу ограниченной функции f(х) необходимо и достаточно, чтобы эта функция являлась измеримой функцией (в смысле Лебега), что эквивалентно существованию мер Лебега всех множеств вида Е_к. Т. к. функции, обычно использующиеся в математическом анализе, измеримы в смысле Лебега, для ограниченных функций Лебег решил задачу определения интеграла исчерпывающим образом.

Из существования для ограниченной функции f(х) интеграла, понимаемого в смысле Римана, следует существование интеграла, понимаемого в смысле Лебега, и их равенство. Обратное неверно - среди функций, интегрируемых в смысле Лебега, имеются всюду разрывные и потому неинтегрируемые по Риману функции, например функция Дирихле f(х), равная нулю для иррациональных х и равная единице для рациональных х.

Для распространения понятия интеграла в смысле Лебега на неограниченные функции для неограниченной измеримой функции f(х) вводится срезанная функция [f(х)]^В_А, равная f(х) при х таких, что А ≤ f(х) ≤ В, равная А при х таких, что f(х) < А, и равная В при х таких, что f(х) > В. Интеграл  (1) от неограниченной измеримой функции f(х) определяется как предел понимаемого в смысле Лебега интеграла (1) от функции [f(х)]^В_А, когда А≠∞, В ≠ ∞ независимо друг от друга, если этот предел является конечным. В этом случае функция f(х) называется интегрируемой по Лебегу (или суммируемой) на отрезке [а, b].

Если для последовательности интегрируемых по Лебегу на отрезке [а, b] функций f(х), f₂(х), ... для каждого ε>0 существует число N такое, что для всех n, m > N выполняется условие

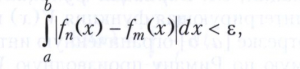
то существует интегрируемая по Лебегу функция f(х), для которой

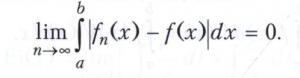
Для функций, интегрируемых по Риману, подобное свойство, вообще говоря, не выполняется.

Понятие интеграла в смысле Лебега обобщается и на случай интеграла по полупрямой и всей бесконечной прямой. После таких обобщений теория интеграла в смысле Лебега охватывает все случаи абсолютно сходящихся несобственных интегралов.

Общность, достигнутая при введении интеграла в смысле Лебега, существенна для многих разделов математики и её приложений. Например, только используя интеграл в смысле Лебега, можно установить изоморфизм двух гильбертовых пространств, пространства L₂[а, b], элементами которого являются все функции f(х), для которых существуют интегралы ∫^b_a|f(х)|²dx, и пространства l₂, элементами которого являются все последовательности {х1, х2, ...}, для которых сходится ряд ∑^∞_k=1|x_k|². Указанный изоморфизм устанавливает связь между волновой механикой Э. Шрёдингера и матричной механикой В. Гейзенберга.

Интеграл Стилтьеса. В 1894 Т. Стилтьесом было дано другое обобщение интеграла в смысле Римана. Пусть f(х) - непрерывная на отрезке [а, b] функция действительной переменной х, а функция V(х) ограниченна и монотонна (т. е. либо не убывает, либо не возрастает) на этом отрезке. Для произвольного разбиения отрезка [а, b] точками (2) и произвольного выбора точек ξ_k на частичных отрезках [x_k-1, x_k] вместо суммы (3) составляется сумма

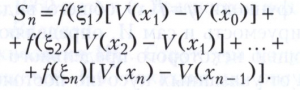
Для непрерывной функции f(х) предел сумм S_n при стремлении к нулю наибольшей из разностей x_k-x_k-1 обозначается символом

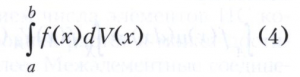
и называется интегралом в смысле Стилтьеса (или Римана - Стилтьеса) от функции f(х) относительно функции V(х) (на отрезке [а, b]). При этом V(х) называется интегрирующей функцией. Интеграл  в смысле Стилтьеса (4) существует и в случае, когда ограниченная интегрирующая функция V(х), не будучи монотонной, представима в виде разности двух ограниченных монотонных функций V₁(х) - V₂(х) (т. е. является функцией ограниченной вариации, смотри Вариация функции). Если интегрирующая функция V(х) имеет на отрезке [а, b] ограниченную интегрируемую по Риману производную V’(х), то интеграл в смысле Стилтьеса (4) сводится к интегралу в смысле Римана по формуле

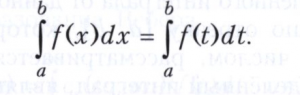
В частности, при V(х) = х + С интеграл в смысле Стилтьеса превращается в обычный интеграл в смысле Римана. Рассматривается также интеграл Лебега - Стилтьеса.

Дальнейшие обобщения. Обобщения понятия интеграла, данные Т. Стилтьесом и А. Лебегом, в дальнейшем удалось объединить и перенести на интегрирование по любым измеримым множествам в многомерных пространствах. Такое обобщение охватывает классические кратные интегралы.

Потребности теории вероятностей, теории динамических систем, спектральной теории дифференциальных операторов привели к понятию абстрактного интеграла Лебега, основанному на общих понятиях теории меры.

Пусть Х - пространство, в котором выделена система В его подмножеств, обладающая свойством замкнутости по отношению к обычным теоретико-множественным операциям, производимым в конечном или счётном числе (т.е. В является σ-алгеброй), μ - заданная на В конечная мера.

Сначала определяется интеграл по пространству Х от В - измеримой кусочно постоянной функции у = f(х), то есть функции, принимающей конечный или счётный набор значений у₁, у₂,... соответственно на попарно непересекающихся множествах A₁, А₂,...є В, объединение которых есть Х. Он определяется как сумма ряда ∑^∞_k=1y_kμ(A_k)при условии, что этот ряд является абсолютно сходящимся, и обозначается символом ∫_Х f(х)μ(dx).

Для функции у = f(х) общего вида интегрируемость и сам интеграл определяются с помощью некоторого предельного перехода от указанных кусочно постоянных функций. Если А - измеримое множество, т. е. А є В, функция Y_A(х) = 1 для х є А, и Y_A(х) = 0 для х ∉ А, то интеграл от f(x) по множеству А определяется равенством

При фиксированных μ и А интеграл от f может рассматриваться как линейный функционал; при фиксированной f интеграл, как функция множества А, является счётно аддитивной функцией.

Все приведённые выше обобщения понятия интеграла таковы, что функции f и |f| оказываются интегрируемыми или неинтегрируемыми одновременно.

А.Данжуа (1912) и немецкий математик О. Перрон (1914) ввели более общий процесс интегрирования, чем лебеговский, который полностью решает задачу восстановления функции по её точной конечной производной. Дальнейшие расширения понятия интеграла были независимо предложены А. Данжуа (1916) и А. Я. Хинчиным (1916). О других обобщениях понятия интеграла смотри в статье Несобственный интеграл.

Лит.: Лебег А. Интегрирование и отыскание примитивных функций. М.; Л., 1934; Камке Э. Интеграл Лебега-Стилтьеса. М., 1959; Уитни Х. Геометрическая теория интегрирования. М., 1960; Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. 7-е изд. М., 2004; Сакс С. Теория интеграла. М., 2004.