Деление

ДЕЛЕНИЕ, математическая операция, обратная умножению, заключающаяся в нахождении одного из двух сомножителей, если известны произведение и другой сомножитель. Таким образом, разделить число а на число d - значит найти такое число х, что xd = а. Результат деления х называется частным, или отношением a и d, заданное произведение а - делимым, а заданный множитель d - делителем. Для обозначения деления употребляют знаки двоеточия (а:d) и горизонтальной или наклонной черты.

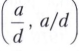
Знак двоеточия введён Леонардо Пизанским (1202), горизонтальной черты - английским математиком У. Джонсом (1633). Термины «деление», «делитель», «делимое» впервые употребляются у французского математика Герберта в конце 10 века, «частное» - у Леонардо Пизанского в 1202. Соответствующие русские термины ввёл Л. Ф. Магницкий (1703).

В пределах множества целых чисел деления не всегда возможно (6 делится на 2 и 3, но не делится на 5), но в тех случаях, когда оно возможно, результат его определён единственным способом (однозначно). В множестве всех рациональных (целых и дробных) чисел деление не только однозначно, но и всегда осуществимо, за исключением деления на нуль. Если исходить из данного выше определения деления, то деление числа, отличного от нуля, на нуль невозможно. Результатом деления нуля на нуль, по этому определению, может быть любое число, т.к. с·0 = 0 для любого числа с. Обычно в математике считают, что деления на нуль невозможно во всех случаях.

Наряду с точным делением, которое рассматривалось выше, используется деление с остатком. Это, по существу, особая операция, отличная от деления в определённом выше смысле. Если a и d - целые положительные числа, то операция деления с остатком числа а на число d состоит в нахождении целых неотрицательных чисел х и у таких, что а = xd + у, у < d. Эта операция всегда осуществима и однозначна. Если у = 0, то говорят, что а делится на d без остатка. Существуют простые признаки делимости без остатка на некоторые положительные числа. Признак делимости целого положительного числа а на целое положительное число d - это условие, которому удовлетворяет а в том и только в том случае, когда оно делится на d без остатка. Желательно, чтобы это условие было легко проверить и чтобы эта проверка была не сложнее непосредственного деления числа а на d.

Пусть число а записано в десятичной системе счисления а = a_n...a₂a₁a₀, т.е. а = а₀+10а₁+ 10²а₂ + ... + 10 ⁿа_n.

Из этого представления получаются признаки делимости на делители чисел 10, 100, 1000, ... В частности, для того чтобы число а делилось на 2, необходимо и достаточно, чтобы его последняя цифра а₀ делилась на 2, т.к. число а - а₀ = 10а₁ + 10²а₂ + ... + 10ⁿа_n делится на 2. Для того чтобы а делилось на 4, необходимо и достаточно, чтобы а₀ +10a₁ делилось на 4, т.к. а - а₀- 10a₁ = 10²а₂+ ...  + 10ⁿа_n делится на 4. Аналогично, а делится на 8 тогда и только тогда, когда a₀ + 10а₁ + 100а₂ делится на 8. Т. к. разность (а₀+10a₁) - (а₀ +2a₁) делится на 4 и, значит, числа а₀ + 10a₁ и а₀ + 2a₁ делятся на 4.

Каждый признак делимости на число d сопоставляет числу а, если оно не слишком мало, некоторое неотрицательное число, меньшее а, которое делится на d тогда и только тогда, когда само а делится на d. Другими словами, каждый признак делимости на число d определяется некоторой функцией f, принимающей целые значения и удовлетворяющей условию |f(а)| < а для каждого целого положительного а, начиная с некоторого, причём f(а) делится на d тогда и только тогда, когда а делится на d. Функция, удовлетворяющая этим условиям, называется функцией делимости на число d, множество всех таких функций обозначается Ω(d). Перечисленные выше признаки делимости можно представить следующим образом:

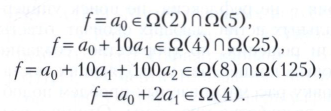
Т. к. 10^k, k= 1, 2 , ..., при делении на 3 и 9 даёт в остатке 1, число а = а₀ + 10а₁ + ... ... + 10ⁿа_n представимо в виде а = а₀ +  а₁ + ... + а_n + b, где b делится на 9. Поэтому а делится на 3 (на 9) тогда и только тогда, когда сумма его цифр а₀ + а₁ + ... +a_n делится на 3 (на 9), т. е. соответствующая функция делимости

Целое положительное число, большее единицы, называется простым, если оно не делится без остатка ни на одно целое неотрицательное число, отличное от единицы и самого себя, в противном случае оно называется составным. Любое целое число, большее единицы, можно разложить в произведение простых чисел, например, 924 = 2·2·3·7·11, причём это разложение единственно с точностью до порядка множителей. Данное число n делится на простое число р в том и только в том случае, если р встречается среди простых множителей, на которые разлагается n.

Для двух целых положительных чисел среди всех их общих делителей существует наибольший, называемый наибольшим общим делителем. Если наибольший общий делитель двух чисел равен единице, то числа называются взаимно простыми. Целое число, делящееся на два взаимно простых числа, делится на их произведение. На этом факте основаны простые признаки делимости на 6 = 2·3, на 12 = 3·4, на 15 = 3·5.

Описанная выше операция деления с остатком аналогично определяется для многочленов вида

Р(х) = а₀х^п + а₁х^п-1 +... + а_п-1 х + а_n.

Она состоит в нахождении по многочленам Р(х) и Q(х) многочленов S(х) и R(х) таких, что Р(х) = S(х)Q(х) + R(х), где степень R(х) меньше степени Q(х). Эта операция также однозначна и всегда выполнима. Если R(х) = 0, то Р(х) делится на Q(х) без остатка. Аналогично теории делимости целых чисел строится теория делимости для многочленов. При разложении многочленов роль простых чисел играют неприводимые (не разлагающиеся на множители) многочлены. Свойство быть неприводимым зависит от того, какие числа допускаются в качестве коэффициентов. При действительных коэффициентах неприводимыми могут быть только многочлены 1-й и 2-й степеней, а при комплексных коэффициентах - только 1-й степени.

Лит.: Курош А. Г. Курс высшей алгебры. 13-е изд. СПб., 2004; Депман И. Я. История арифметики. 3-е изд. М., 2006.